/natureduca/tecnologia-tecnica-informatica-representacion-de-la-informacion-09

---

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

El sistema de numeración binario (continuación)

ara contar en el sistema de numeración binario empezaremos por el 0 y a continuación el 1, pero para designar dos unidades no podemos utilizar el símbolo 2, ya que no existe en dicho sistema. Por tanto, tendremos que utilizar dos cifras binarias (al igual que en el sistema decimal cuando llegamos a 9, el número siguiente lo escribimos con dos cifras: 10).

Luego el número dos se escribirá en base 2 como 10, el tres como 11 y nuevamente necesitaremos otra cifra para representar el cuatro: 100.

La conversión de un número binario a decimal se hace aplicando el teorema fundamental de la numeración o dando valores a las sucesivas potencias de 2:

Así pues, el número binario 110101₍₂ tendrá la expresión decimal siguiente:

110101₍₂= (1 x 2⁵) + (1 x 2⁴) + (0 x 2³) + 3 + (1 x 2²) + (0 x 2¹) + (1 x 2⁰) = (1 x 32) + (1 x 16) + (0 x 8) + (1 x 4) + (0 x 2) + (1 x 1) = 53₍₁₀

es decir, el número binario 110101 es igual al número decimal 53.

Las tablas de sumar y multiplicar son:

+ 0 1 * 0 1
0 0 1 0 0 0
1 1 1 1 0 1

A continuación, se muestran algunos ejemplos de sumas y multiplicaciones binarias:

Existen varios tipos de códigos binarios, pero por su sencillez y utilidad, por ahora sólo mencionaremos el llamado código binario BCD(Binary Coded Decimal). Más adelante, se describirán otros códigos binarios de uso frecuente.

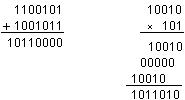
Para designar en código BCD a un número decimal de un dígito se emplean cuatro dígitos según la siguiente equivalencia:

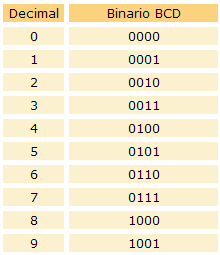
Para designar números decimales de varios dígitos en código BCD, se representa cada dígito decimal por su correspondiente BCD.

Por ejemplo, representar en código binario BCD el número decimal 365:

por tanto será 001101100101 en código BCD.

Nótese que la representación en código binario BCD, no coincide con la expresión del mismo número decimal en binario puro, que para el ejemplo dado sería la siguiente:

365₍₁₀ = 101101101₍₂

por tanto, la codificación en binario BCD no es un cambio de base del sistema de numeración empleado, sino una codificación convenida para representar los números en sistema decimal mediante expresiones que no contienen más que 0 y 1.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16

© ASOCAE ONGD, Asociación Española para la Cultura, el Arte y la Educación - www.asocae.org - RNA 592727 - CIF.: G70195805 ¦  Quiénes somos  ¦  Contacto  ¦  Bibliografía ¦  Política de privacidad ¦ Esta web NO utiliza cookies, ni guarda datos personales de los usuarios